Linear motion in two voices
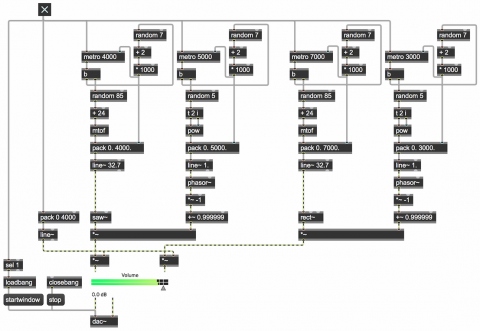
Two oscillators, one in the left channel and one in the right channel, play notes that have a continuously changing frequency, at a continuously changing note rate. Every few seconds (some randomly-chosen number of seconds from 2 to 8) each of the two oscillators gets a new destination frequency and destination note rate, and heads toward those destination values over the next few (randomly-chosen number of) seconds.
You can see a couple of useful Max tricks in the lower left corner of the patch. We use loadbang to turn on audio automatically so that the user doesn't need to think about that. (The startwindow message to dac~ turns on audio locally in that one window, without turning it on in the rest of Max.) We also use a select object (a.k.a. sel) to detect when the toggle is turned on, to make extra sure that audio is on. That's not strictly necessary, and is a little redundant, but it's always possible that audio could get turned on or off in another window somewhere after this patch is opened, so we put this in just in case. The startwindow message turns off audio in other windows, so that you only hear this window. We use pack, line~, and *~ to do a 4-second fade-in/fade-out each time the toggle is turned on or off, just to make the beginning and ending a bit more graceful.
The rest of the patch is the part that makes the sound. There are two soundmaking portions, and they're nearly identical, so let's just look at one of them.
We use a saw~ object to generate a band-limited sawtooth waveform*, like an old-school synthesizer. The sawtooth oscillator gets its frequency from a line~ object (set at 32.7 Hz initially, which is the low C of the piano). The amplitude of the sawtooth is controlled by a phasor~ which is inverted (multiplied by -1) and then pushed back into the positive range (is offset by nearly 1)** so that, instead of ramping from 0 up to 0.999999 then leaping back down to 0, it now leaps up to 0.999999 and ramps back down to 0, making a nice sudden percussive attack and a smooth decay when used as an amplitude envelope. So this phasor~ is actually being used to shape the amplitude of the saw~, in effect playing individual notes of sawtooth sound. The rate of the phasor~ is controlled by a line~ object (set at 1 Hz initially).
The value of those two line~ objects will be continually changing based on the four objects just above them. The frequency of the oscillator is determined by the output of the line~, and the destination value of the line~ is determined by a random pitch from piano low C to piano high C. We choose a random MIDI key number from 0 to 84, add 24 to it so that it's now in the range 24 to 108, and then convert that to a frequency using the mtof (MIDI to frequency) object, a simple algebraic equation.*** That frequency destination value gets combined with a ramp time in pack and sent to line~ as a "destination value" and "ramp time" pair. The note rate is calculated in a similar manner. We choose a random number 0 to 4, and use that as a power of 2. That is, we use it as the exponent in the pow object, with a base of 2, to calculate 2 to the n power. The result will be 1, 2, 4, 8, or 16 notes per second. That note rate destination value gets combined with a ramp time and sent to line~.
At the top, we have a metro with an initial time interval of 4000 ms (the same as the initial destination time in the pack object). When the metro sends a 'bang', we send a new frequency instruction to line~, as described in the previous paragraph. Then we randomly choose a number from 0 to 6, add 2 to it, and multiply that by 1000, to get a random number of seconds from 2 to 8 (2000 to 8000 ms). We use that time interval to prepare for the ramp time of the next instruction to line~, and to set up the interval for the next scheduled output of the metro. In this way, the ramp time of line~ and the rate of the metro changes to some (usually different) number of seconds with every output. The exact same sort of operation is done with the metro and line~ objects controlling the note rate. The fact that we're using a different metro and a different random object means that the two metros for frequency and note rate are independent and not really in sync, except for the fact that they are always using some whole number of seconds as their interval so they occasionally will coincide recognizably.
The sound generator for the right channel is nearly identical, except that it uses a band-limited square wave oscillator****, rect~, as its sound source, so its sound will be distinguishable from that of the saw~ object. All four metros are initially set to mutually prime time intervals, so that they start out not being in sync with each other. However, because the random objects are choosing from the same relatively small number of time intervals, the sums of their chosen time intervals occasionally match, so that we sometimes get fortuitous coincidence of some aspect of the two sounds. This gives the impression that there is some intentionality or organization, and in fact there is -- the time values were chosen intelligently by the programmer -- just enough to keep the music engaging. Likewise, the limited range of choices for destination note rate (1, 2, 4, 8, or 16 notes per second) causes the tempo of the two note-generators to converge occasionally in interesting ways.
For simplicity, I didn't add in any more complexity that might have made the sounds themselves more interesting, but you can probably imagine some modifications that might make this patch even more sonically/musically interesting: filter envelopes on each note, slow filter sweeps, small delays, echoes, time-varying delays, reverb, etc. Heck, what about dynamics? At present there's no variation in amplitude. Any perceived variation in loudness is really just due to our frequency-dependent perception and cognition. Despite the somewhat annoyingly simplistic sounds, I find that this simple algorithm produces a continuously changing counterpoint that remains interesting, if not expressive, for at least a minute or two.
* A sawtooth wave is described in MSP Tutorial 3. A sawtooth is a waveform that contains all the harmonics of the fundamental frequency, with amplitudes inversely proportional to the harmonic number. The 2nd harmonic has 1/2 the amplitude of the 1st harmonic, the 3rd harmonic has 1/3 the amplitude, etc. So, it's richer and buzzier than a sine tone. The phasor~ object makes a kind of idealized sawtooth shape, which is useful as a control signal, but it's not so great as an audio wave because it has, theoretically, infinite harmonics and can therefore cause aliasing. For that reason, MSP includes an object called saw~ that uses a different formula to calculate a waveform that sounds similar to a sawtooth, but that does not produce harmonics above the Nyquist frequency (half the sampling rate).
** Although it's easy to say that a phasor~ object makes a ramp from 0 to 1, it's more accurate to say that it goes from 0 to almost 1. The output of phasor~ is calculated by continuously interpolating between 0 and 1 based on its rate. It never actually sends out a signal of 1, because at that point it wraps back around to 0. (And depending on how fast it's going, you can't rely on it outputting a true 0 either, since that 0 might fall in between successive samples.) Thus, the actual range of phasor~, based on 32-bit floating point calculations, is 0 to 0.999999.
*** f equals 440 times (2 to the (m-69)/12 power), if you really must know.
**** An ideal square wave produces all the harmonic frequencies of the fundamental in inverse-square proportion to the harmonic number. For example, the 2nd harmonic has 1/4 the amplitude of the 1st harmonic, the 3rd harmonic his 1/9 the amplitude, etc. Thus, it's somewhat less bright and buzzy than a sawtooth wave. Similarly to saw~, the rect~ object uses a different formula to calculate a waveform that sounds similar to a square wave, but that does not produce harmonics that would cause aliasing.