Repeatedly reading a function with phasor~

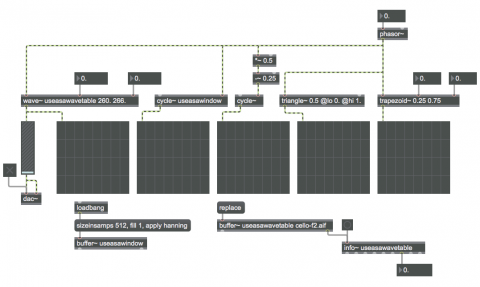
The real value of phasor~ is that it provides a very accurate way to read through (or mathematically calculate) some nonlinear shape to use as a control signal (or even as an audio signal). Among other things, it might be used to create a "window" shape that can serve as an amplitude envelope for a sound. This patch demonstrates five different ways to create window or waveform shapes with phasor~. We'll discuss them (in good Max fashion) from right to left.

The trapezoid~ object expects a signal that progresses from 0 to 1. It has two arguments (or values it can receive): one to say at what point its upward ramp should end, and the other to say at what point its downward ramp should begin. So in this example, as the phasor~ signal goes from 0 to 1, the trapezoid~ object will ramp upward and arrive at 1 just as phasor~ gets to 0.25 (the first argument of trapezoid~), then trapezoid~ will stay at 1 until phasor~ gets to 0.75 (the second argument of trapezoid~) at which point trapezoid~ will begin to ramp back down to 0 and will arrive there just as phasor~ completes its cycle. This can be useful for tapering the ends of some other signal (such as notes or loops played by a groove~ object) to avoid clicks.

The triangle~ object similarly makes a simple shape when driven by a signal between 0 and 1. The first argument of triangle~ specifies where in the phasor~'s 0-to-1 range the highpoint of the triangle should occur, and the ‘lo’ and ‘hi’ attributes specify the minimum and maximum output values.

The output of phasor~ can be used to control the phase offset of a cycle~ object (in cycle~'s right inlet). If the cycle~'s frequency is 0, the signal from phasor~ will specify the exact location (on a scale from 0 to 1) in the wavetable that cycle~ will send out. Since cycle~ uses a cosine wavetable by default, scanning through the entire wavetable (0 to 1) in this way would cause cycle~ to output a cosine wave. However, in this example we scale and offset the phasor~ signal so that it goes cyclically from -0.25 to 0.25, thus cycling through the first half of a sine wave. This creates a window shape that's commonly called a cosine window, which is also useful as an amplitude envelope, particularly for short notes.

Because the cycle~ object can use a buffer~ as a wavetable, we can fill a buffer~ with 512 samples of any shape we want, and then read through that function with cycle~. The buffer~ object even has a few messages for doing just that. In this patch we have created a buffer~ called "useasawindow", we set its size to 512 samples, we fill it with all values of 1, and then we impose a "hanning" (or "Hann") window on it. (A hanning window is really just cosine waveform that has been scaled and offset.)

The wave~ object can also access samples in a buffer~ in a fashion similar to a cycle~ (with frequency 0) driven by a phasor~. A difference with wave~ is that it can use any portion of a buffer~ as its wavetable. You specify the start and end points (in ms) of the portion of the buffer that you want to use, and wave~ will use that as its wavetable to read when it is driven by a signal from 0 to 1. In this patch we use a small portion (about one cycle) of a cello note. When phasor~ is at a very low sub-audio frequency (such as 1 Hz.) you can see the waveform pretty clearly in the scope~. To hear it, raise the phasor~ to an audio frequency (and turn up the gain~). As you change the range of the buffer~ that is being accessed by wave~, the timbre of the tone will change (because the resulting waveform is changing), but the fundamental frequency of the wave is still largely determined by the rate of the phasor~.