Mixing and crossfading
Mixing or blending two things—whether it’s two sounds or two videos—just means taking a certain amount of thing A and a certain amount of thing B and adding them together.
If you take a full dose of A and a full dose of B—let’s say, a full amplitude sine wave and a full amplitude square wave—and add them together, you’d likely end up with a sum that has an amplitude (or a brightness in the case of video) that’s twice as great as either of them alone. That’s why it’s common to scale A and B down by a certain amount (multiply them by some amount less than 1) so that their sum will eventually equal 1. For example if you multiply the sine tone’s amplitude by 0.25 and the square wave’s amplitude by 0.75, the peak amplitude of their sum will not exceed 1 (and the amplitude of the square wave’s contribution to the mix will be 3 times as great as that of the sine wave).
If you gradually change the level (the multiplier factor) of thing A from 1 to 0, it will fade away from full to none. Conversely, if you gradually change the multiplier applied to thing B from 0 to 1, it will fade from off to full on. If you do both things simultaneously, you get a crossfade from A to B. This is commonly achieved by linearly interpolating the amplitude multiplier of thing A from 1 to 0 (using the output of a line~ object as the multiplier, for example) and using 1 minus that amount as the multiplier for thing B. That ensures that A and B will fade in opposite directions, and that the sum of the two multipliers will at all times be 1.
For examples and explanations of abstractions for basic audio mixing/crossfading, see the following two examples:
A useful subpatch for mixing and balancing two sounds
Mix two signals (more efficiently)
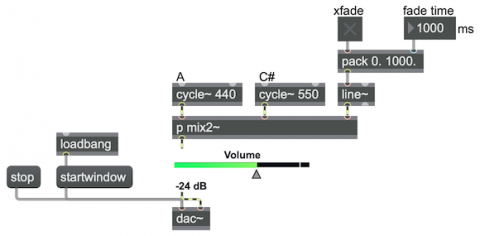
The example patch employs the second of those two mixing algorithms, encapsulated in a subpatch, and shows the use of the line~ object to cause a crossfade from one sound to another.
Note that this example demonstrates a linear mixing system (a linear crossfade from A to B), which is very simple and direct and works for many situations, but may not always be the most desirable way to get from A to B in all circumstances. A straight line is one very special kind of curve—the most direct path possible between two points. One could use any curve of transition other than a straight line. The curve that’s used for mixing two signals is called the law; different laws are used for different effects. Commonly an exponential curve is used, to compensate for our tendency to perceive relative to the logarithm of the stimulus (known as Fechner’s law).