Triggering events with each cycle of a phasor~

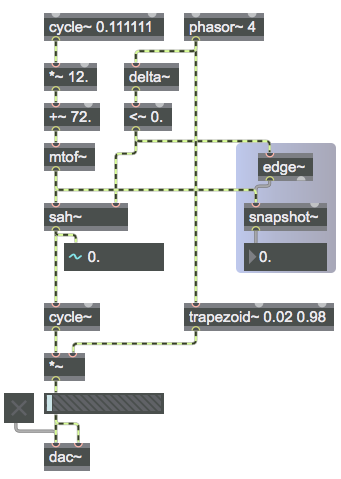
How do we detect, with sample-accurate precision, the precise moment when phasor~ begins a new cycle from 0 to 1? We need to detect the sample on which it leaps from 1 back to 0. However, because phasor~ is constantly interpolating between 0 and 1, it might not leap down to exactly 0. So we can't just use a ==~ object to see when its value is 0. Its exact value is relatively unknowable with any great precision; all we know is that it's always increasing...except at the one instant when it leaps back down to (approximately) 0 and begins again. However, that instant is so remarkable that there is a way to detect it, with the help of an object called delta~. A delta~ object sends out a signal in which each sample reports the change in its input relative to the previous sample. So, if we send a phasor~ into a delta~, delta~ will always report a positive increase (or 0 if the phasor~ is completely stopped), except for when the phasor~ leaps downward. That's the one sample on which delta~ will report a negative value. So we can use a <~ ‘0’ object to detect the sample on which that occurs. The <~ ‘0’ object will always output a signal of 0 (false) except for that one sample when it will report a 1 (true).

The sah~ object implements a "sample-and-hold" mechanism. When a particular threshold is surpassed in the signal in its right inlet, it will sample the value of the signal in its left inlet and will hold that as a constant output signal value until the next time the threshold is surpassed in the right inlet. By default its threshold is 0, so every time the <~ ‘0’ object sends out a 1 preceded by a 0 it will cause sah~ to sample its left input. We use that fact to sample the slowly moving sinusoidal control value coming from cycle~ via mtof~. The cycle~ is moving slowing with a period of 9 seconds, and it's varying + or - 12 semitones from a central pitch of 72 (C above middle C); that signal value is converted to frequency by the mtof~ (MIDI to frequency) object and that is sampled and held 4 times per second by the sah~ which is triggered by the phasor~. That frequency value from sah~––which is constant for each 1/4 second until it is changed by sah~––is used by cycle~ as its frequency value for its notes.

The individual notes are shaped by a trapezoidal amplitude envelope. The envelope is almost rectangular, but it has a very quick ramp up and down during the first and last 2% of each note (5 ms in this case). Because the change in frequency of the cycle~ that we're listening to is triggered by the beginning of each cycle~ of the phasor~, it's perfectly synchronized with the trapezoidal amplitude envelope.

If you want to use the beginning of a phasor~ ramp to trigger events in other parts of a Max patch, you can use an edge~ object to detect the 1 values coming from the <~ ‘0’ object. The edge~ will send out a bang when a 0-to-1 or 1-to-0 transition occurs in a signal vector. But it can only do so with as much precision as the Max scheduler provides, which is not sample-accurate. So in this patch we use edge~ to detect the 0-to-1 transitions, then we use that bang to trigger a report of the current frequency value with a snapshot~ object. Note that not only will the edge~ object not send a bang with sample-rate precision, snapshot~ will only report the value at the beginning of the signal vector when (or immediately after) it receives the bang. So these translations between the sample-accurate-but-vector-based timing of MSP and the millisecond (or vector-based) timing of the Max scheduler show the slight difference between the true sample-accurate timing of the phasor~ and the close approximation that we can achieve with edge~. When you stop the audio (by turning off the dac~), you will probably notice a slight difference between the actual frequency being reported by the number~ object and the frequency reported by snapshot~ at the beginning of the vector when it was triggered by edge~. In many cases this difference is negligible, but in some cases it can lead to clicks when sudden changes are made in an audio signal that is not at 0 amplitude.