Simple wavetable synthesis
One of the earliest methods of digital sound synthesis was a digital version of the electronic oscillator, which was the most common sound generator in analog synthesizers. The method used was simply to read repeatedly, at the established sample rate, through a stored array of samples that represent one cycle of the desired sound wave. By changing the step size with which one increments through the stored wavetable, one can alter the number of cycles one completes per second, which will determine the perceived fundamental frequency of the resulting tone. For example, if the sample rate (R) is 44100 and the length of the wavetable (L) is 1000 samples, and our increment step size (I) is an expected normal step of 1, the resulting frequency (F) will be F=IR/L which is 44.1 Hz. If we wanted to get a different value for F, while keeping R and L constant, we can just change I, the step size. For example, if we use an increment of 2, leaping over every other sample, we'd get through the table 88.2 times in one second. Thus, by changing I, we can get a cyclic tone of any frequency, and it will have the shape of the waveform stored in the wavetable. (When I is a non-integer number, it will result in trying to read samples at non-existent fractional indices in the wavetable. In those cases, some form of interpolation between adjacent samples is used to get the output value.)
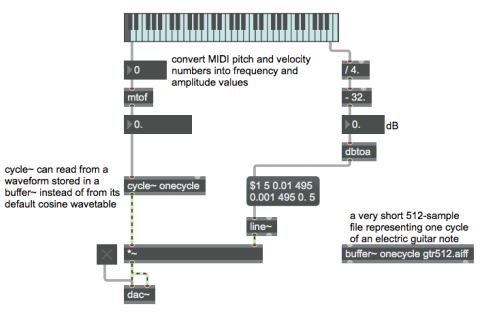
When a cycle~ object refers to a buffer~ by name, it uses the first 512 samples of that buffer~ as its waveform, instead of using its default cosine waveform. In this example, the buffer~ is loaded with a 512-sample file that is actually a single cycle of an electric guitar note. (The file is in the Max folder of your hard drive, which is probably already included in your file search path, so it should load in automatically.) The frequency value supplied in the left inlet of cycle~ determines the increment I value that cycle~ will use to read through that wavetable. So for this example, we use a MIDI-type pitch number from the left outlet of the kslider and convert it to frequency with the mtof object (which uses a formula such as [expr 440.*pow(2.\,($f1-69.)/12.)] to convert from MIDI pitch number to frequency in Hz). We also use the MIDI-type "velocity" value from the kslider to determine the amplitude of the sound. The velocity value is scaled and offset to give a decibel range between -32 dB and 0 dB; that is used as the peak (attack) amplitude in an amplitude envelope sent to the line~ object to control the amplitude of the cycle~. The amplitude envelope goes to the peak amplitude in 5 ms, then falls to 0.01 (-40 dB) in 495 ms, then falls further to 0.001 (-60 dB) in 495 more ms, and finally goes to 0. (-infinity dB) in 5 ms; so the whole envelope shapes a 1-second note.
Notice that when you play high notes on the keyboard, the tone becomes inharmonic. That's because the stored waveform in the buffer~ is so jagged and creates so many harmonics of the fundamental pitch. When the fundamental is high (in the top octave of this keyboard the fundamental frequencies are all above 1000 Hz) upper harmonics of the tone get folded back due to aliasing, resulting in pitches that don't belong to the harmonic series of the fundamental.