Multiplication of sinusoidal tones

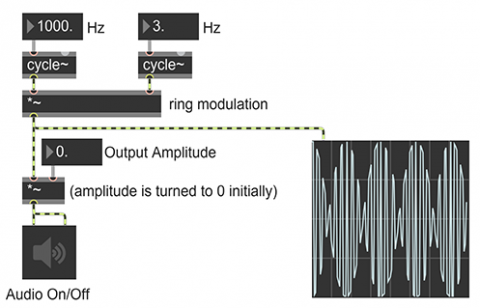
Multiplying one tone by another, in effect, imposes the contour of one waveform on that of the other waveform. For example, mutiplying a 1000 Hz sinusoidal tone by a 3 Hz sinusoidal tone yields something very much like a 1000 Hz sine tone, but with its amplitude continually shaped by the low-frequency oscillator (LFO). Because the LFO goes from 0 to 1 to 0 to -1 to 0 each cycle, the amplitude of the 1000 Hz tone goes from 0 up to 1 and back down to 0, then to -1 and back to 0 for each cycle of the LFO. We don't distinguish auditorily between negative and positive amplitudes, so to us it sounds like the sound is pulsating twice per cycle of the LFO, which, with a 3 Hz LFO, is 6 times per second.

An important fact about multiplication (ring modulation) of two sinuosoids is that the result is mathematically equivalent to adding two half-amplitude sinusoids at the sum and difference frequencies of the two tones. That is, if you multiply a 1000 Hz sinuosoid and a 3 Hz sinusoid, the result is a 1003 Hz sinusoid (the sum of the two frequencies) and a 997 Hz sinusoid (the difference of the two frequencies). The difference between those two tones is, of course, 6 Hz, which is another way of understanding the 6 Hz beating effect.

Ring modulation is a particularly useful effect when one of the two tones is a complex tone containing many frequencies; the modulation creates a sum and difference frequency for each of the component frequencies, radically changing the harmonic content of the tone.