Animating 2D graphics
In working with video and animation in Jitter, it’s important to remember that the effect of continuous motion is achieved by successive discrete images, each somewhat different from the preceding one. You can create that effect in 2D animation by repositioning graphic objects for each frame, according to a particular trajectory, such that the objects seem to be moving.
Here’s a simple demonstration of that idea. A purple circle will seem to move diagonally from the left-top corner of the window to the right-bottom corner because its x and y coordinates are being changed constantly according to a linear trajectory.
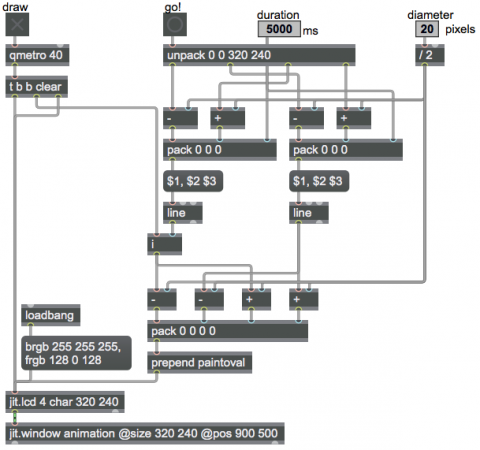
Before writing the program, I made the decision that I wanted it to move a purple dot diagonally across the full size of the window from coordinate 0,0 to coordinate 320,240. In a more sophisticated program, it would be nice if the object could be moved from any point to any other point; but for simplicity, I decided this program would have just one move it knew how to do. So I typed those coordinates into a single object, unpack, which takes items of a list and sends them out individual outlets in right-to-left order. In order to demonstrate how to have some variable possibilities in a program, though, I made it so that the speed and size of the dot could easily be altered.
This sort of automated animation of graphics requires a bit of arithmetic calculation to construct messages that have the right arguments. I decided that the line objects should provide the horizontal and vertical coordinates for the center of the circle, and the program would calculate all the necessary coordinates for the bounding square that would tell jit.lcd where to paint it. The diameter of the circle is specified by a live.numbox, which sends out the number 20 initially, and is limited between 2 and 80. The duration of the trajectory for the two line objects is specified by the other live.numbox; it’s 5000 ms by default, and is limited between 500 and 20000.
When the patch is loaded, the duration value 5000 is stored in the right inlet of the pack objects, and the diameter value 20 is divided by 2 to get the radius and then is stored in the right inlet of all the + and – objects. Also, the loadbang object sets the background color to white (not really necessary, since that’s the default color for jit.lcd anyway) and the foreground color (i.e., the pen color) to purple. When you turn on the toggle labeled “Draw”, at first you won’t see anything happen because the jit.lcd object will receive the message ‘paintoval 0 0 0 0′, which draws an infinitely small oval.
When you click the the button labeled “Go”, it constructs messages to the line objects telling them, “Start at a point that’s radius pixels above and to the left of the window (just outside the left-top corner of the visible window area) and go to a point that’s radius pixels below and to the right of the window (just outside the right-bottom corner of the visible area) in duration milliseconds.” The line objects each send out a number once every 10 ms, and those numbers serve as the horizontal and vertical coordinates of the center point of the circle at each instant. Those coordinates have the radius value subtracted from them or added to them to determine the coordinates of the left-top and right-bottom corners of the bounding square, and those four numbers are combined into a four-item list in a pack object.
There’s one more important little trick, though. The output of the line object on the left doesn’t go directly to the pack object. It’s stored in an int (i) object, and only gets sent out when the i object receives a bang. Every time the qmetro sends a bang, we first use it to erase (clear) the previously drawn object, then we trigger the i object which triggers the left inlet of the pack object which causes a paintoval message to be constructed and sent to jit.lcd, then finally we send the bang to trigger the jit.lcd object to send the new image to jit.window. If you think logically and procedurally about the ordering of these steps, you’ll realize the method by which you can a) erase the previous drawing, b) calculate, construct, and send the messages that will provide the drawing instructions, and then finally, c) send out the matrix.