Time interval and rate

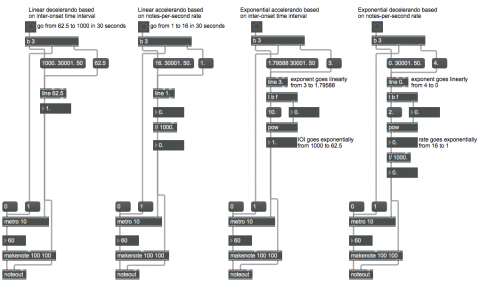
This patch provides examples that compare linear rate changes to exponential rate changes. As with pitch and loudness, our sense of change in the rate of events is based on the ratio of tempos rather than the (subtractive) difference between tempos. In these examples, the rate changes by a factor of 16, from 1 event per second to 16 events per second, or vice versa. In the first example, we use a linear change of time interval for a metro, to go gradually from 62.5 milliseconds to 1000 milliseconds, which is to say from 16 notes per second to 1 note per second. By changing the time interval linearly, we get a larger change in the notes-per-second rate initially than we do later in the accelerando, which means that most of the change in perceived tempo takes place in the earliest part of the thirty seconds. In the second example, by contrast, we use line to effect a linear change in the notes-per-second rate (tempo), which actually causes an increasing rate of change in the time interval being provided to metro, but results in an accelerando that seems (and in fact is) more constant over the course of the thirty seconds, and is thus more musically useful. In the two examples on the left the change, be it of time interval or rate, is linear. In the two examples on the right, the output of line objects is used as the exponent in a pow object, thus converting the linear rate change into an exponential one. This yields, in most cases, a smoother and more "musical" sense of accelerando or decelerando. Exactly which method of change you choose to use depends on which most closely corresponds to the musical effect you're trying to achieve.