Random numbers without repetitions

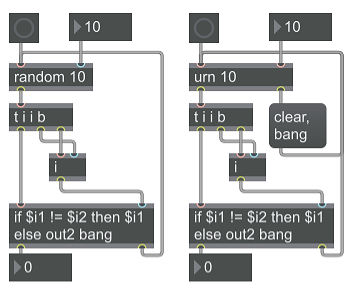
The random object outputs a pseudo-randomly chosen integer. The range of possible numbers is determined by the number received in the right inlet (or specified as a typed-in argument). Each time random receives a bang, it will output one of n possible numbers, ranging from 0 to n-1. Because each number has an equal probability of occurring each time, there’s a possibility that repetitions will occur. If you wish to prevent repetitions there are two approaches.

Instead of random, you can use the urn object, which employs an algorithm that excludes all previously-chosen numbers. Once urn has chosen all possible numbers, if it receives a bang but has no more possible numbers to output, it sends a notifying bang out its right outlet. You can reset urn with a clear message, so that it once again starts choosing from all its possibilities. When you reset it, there's of course the possibility that the first new choice could be the same as the last choice prior to the reset, so if you absolutely want no immediate repeats, you need to test the output and choose again if there's a repeat.

To prevent immediate repetitions, you can store the output of random in a variable (such as int) each time it comes out, and then treat that as the previous number, for comparison with the next output. If the two are the same, you suppress the output and try again (provided you have a minimum of 2 possible random choices, of course).

You can use that same method to prevent repetitions when you reset an urn object, although it’s redundant the rest of the time, since urn already avoids repetitions.

Here’s a little nerdy detail. With the method shown on the left, using the random object, each number always has an equal likelihood of being chosen each time, except for the previous number which has no likelihood of being chosen. Whereas, with the urn object shown on the right, each number that has been chosen since the last reset has a zero likelihood of being chosen, and the remaining unchosen numbers have an increasing likelihood of being chosen.