Random note choices

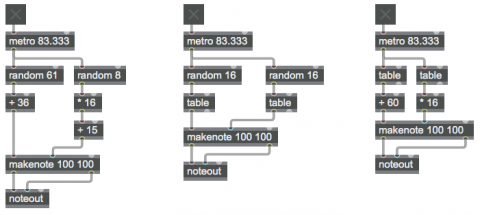
The left part of this example shows the use of the random object to make arbitrary note choices. Every time random receives a bang in its inlet, it sends out a randomly chosen number from 0 to one less than its argument. In this case it chooses one of 61 possible key numbers, sending out a number from 0 to 60. We then use a + object to offset that value by 36 semitones, transposing up three octaves to the range 36 to 96––cello low C to flute high C. Similarly, we choose one of 8 possible velocities for each note. The random object sends out a number from 0 to 7, which we scale by a factor of 16 and offset by 15, thus yielding 8 possible velocities from 15 to 127. These choices by the random objects are made completely arbitrarily (well, actually by a pseudo-random process that's too complex for us to detect any pattern), so the music sounds incomprehensible and aimless.

One can make random decisions with a little bit more musical "intelligence" by providing the computer with a little bit of musically biased information. Instead of choosing randomly from all possible notes of the keyboard, one can fill a table with a small number of desirable notes, and then choose randomly from among those. In the middle example, we have filled lookup tables with 16 possible velocity values and 16 possible pitches. Each time we want to play a note, we choose randomly from those tables. The velocities are mostly mezzo-forte, with only one possible forte value and one fortissimo value. Thus, we would expect that most notes would be mezzo-forte, with random accents occurring unpredictably on (on average!) one out of every eight notes. The pitches almost all belong to a Cm7 chord, with the exception of a single D and a single A in the upper register. So, statistically we would expect to hear a Cm7 sonority with an occasional 9th or 13th. There's no strong sense of melodic organization, because each note choice is made by random with no regard for any previous or future choices, but the limited, biased set of possibilities lends more musical coherence to the results.

In a completely different usage of the table object, you can use table as a probability distribution table, by sending it bang messages instead of index numbers. When table receives a bang, it treats its stored values as relative probabilities, and sends out a chosen index number (not the value stored at that index) with a likelihood that corresponds to the stored probability at that index. Double-click on the table objects in the right part of the patch to see the probabilities that are stored there. In the velocity table, you can see that there is a relatively high probability of sending out index numbers 4 or 5, and a much lesser likelihood of sending out index numbers 1 or 7. These output numbers then get multiplied by 16 to make a MIDI velocity value. Thus we would expect to hear mostly mezzo-forte notes (velocities 64 or 80) and only occasional soft or loud notes (velocities 16 or 112). In the pitch table, you can see that the index numbers with the highest probabilities are 0, 4, 7, and 11 respectively, with a very low likelihood of 2, 9, or 12. These values have 60 added them to transposed them to the middle octave of the keyboard. So we would expect to hear a Cmaj7 chord with only a very occasional D or A.

To learn more about the use of table to get weighted distributions of probabilities, read the blog article on "Probability distribution".