Random and urn

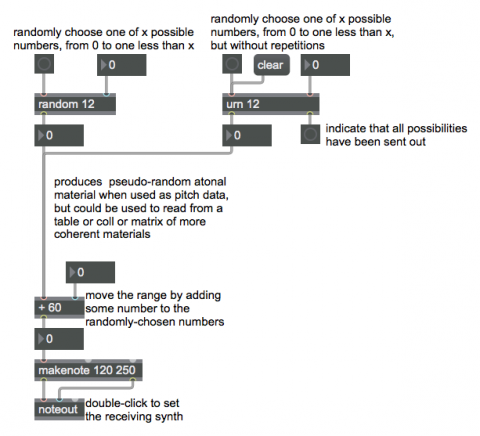
This patch demonstrates the two simplest objects for generating random numbers. Every time it receives a bang in its left inlet, the random object generates a random integer in the range from 0 to one less than its argument. (For example, if you tell it to generate one of 12 random numbers, it will choose a number from 0 through 11 inclusive.) Note that this includes the possibility that successive random choices may appear to generate what seem to be patterns, especially if it's choosing from among a small range of possibilities. That's because repetition is possible. The urn object functions in much the same way, but it always generates a unique number (i.e., it doesn't repeat a number). Once it has no more unique numbers available within the specified range, it sends a bang out its right outlet indicating it has run out of possibilities instead of sending a number out its left outlet. The clear message resets urn. Can you figure out how to make urn reset itself and try again when it's out of numbers to choose?

In this example, the random numbers are used as pitch information, generating an arbitrary atonal melody. That's certainly not the most interesting thing to do with random numbers, but it does demonstrate what arbitrary atonal melody sounds like, and 'sonifies' randomness pretty successfully.

There are several other objects for generating random numbers.

●      drunk generates constrained random integers ("Brownian" motion)

●      expr has a "random()" function for generating random integers in any specified range

●      noise~ generates a MSP signal filled with random (float) numbers between -1 and 1 (white noise)

●      pink~ generates a MSP signal filled with pink noise (like white noise but with diminished high frequency content)

●      rand~ generates band-limited (low-pass filtered) noise by interpolating linearly between more slowly-chosen random numbers

●      jit.noise fills a Jitter matrix with random numbers (of any data type)

My algorithmic composition blog has several chapters on randomness, beginning with (intuitively enough) the chapter titled "Randomness".