Linear frequency vs. linear pitch

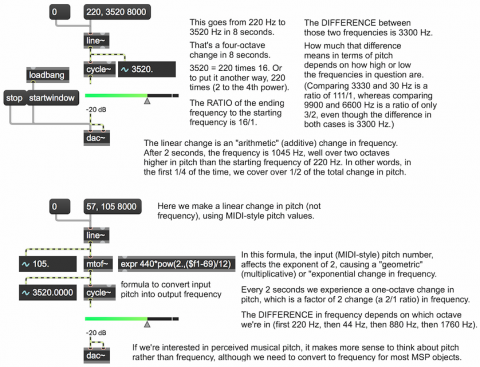
As expressed in Fechner's law, our subjective sensation of a phenomenon is often proportional to the logarithm of the empirical measurements of the intensity of the physical event that evokes that sensation. One example of that in musical contexts is that our sensation of changes in musical pitch are proportional to the logarithm of the change in the measured fundamental frequency of a tone. A linear arithmetic (additive) increase in successive frequencies, such as 100 Hz, 200 Hz, 300 hz, 400 Hz, 500 Hz, etc., would give us an impression of decreasing size of musical pitch intervals between those tones, in this case an octave followed by a perfect fifth followed by a perfect fourth followed by a major third, etc. You can think about this phenomenon in the opposite way, too: In order to give a linear impression of increase in pitch, you would need an exponentially increasing series of frequencies. For example, to give the effect of a linear chromatic ascent of equal-tempered semitones in a melody, the fundmental frequency of the successive tones would have to increase by a factor of the twelfth root of two for each interval.

This patch demonstrates that law. In the top part of the patch, a linear change in frequency is heard, covering a span of 3300 Hz, from 220 Hz to 3520 Hz, in 8 seconds. In the bottom part of the patch, a linear change in pitch is heard (converted to frequency before being sent to the cycle~ object) over the same range of frequency in the same total amount of time. In the former case, we hear a linear change in frequency as a logarithmic change in perceived pitch; the perceived pitch changes more quickly at first, and more slowly later. In the latter case, to get a sense of constant linear change in pitch, we need to use an exponential change in frequency, changing more slowly at first and more rapidly later. Listen to the two glissandi to see if you hear the difference.