Indexing and accessing the bins of an FFT

The Fast Fourier Transform (FFT) is a mathematical procedure for converting a time-domain signal (such as a sound wave) into an equivalent frequency-domain representation (the sound’s spectrum). The inverse transform (IFFT) reverses that process. The Max object pfft~ allows you to encapsulate an FFT and IFFT (with the objects fftin~ and fftout~ respectively) and program some sort of frequency-domain processing (alteration of the spectrum) between the two. The objects fftin~ and fftout~ are like special signal inlet and outlet objects within pfft~.

An audio signal that comes into pfft~ via an fftin~ object gets converted into two signals, representing the real and imaginary (cosine and sine) components of the Fourier analysis. You could think of these as x and y points on a Cartesian plane, one for each frequency bin of the spectrum from 0 Hz to the Nyquist frequency (one half the sample rate). That’s not terribly useful in and of itself, but you can make it more useful by describing those real and imaginary values (the points on the Cartesian plane) in polar form, which is to say as a vector that has a magnitude (the distance from the origin of the plane to the point itself, calculated using the Pythagorean theorem) and a phase angle (the angle of the vector in radians, calculated using the arctangent function). The magnitude and phase angle represent the amplitude and phase of the sinusoidal component for each frequency bin. Those are more intuitive and useful pieces of information about the spectrum. That conversion from real and imaginary components into magnitude and phase angle components is done by the cartopol~ (Cartesian to polar) object. Note that the rightmost outlet of fftin~ sends out a number from 0 to one less than the FFT size, which is the index number of each frequency bin.

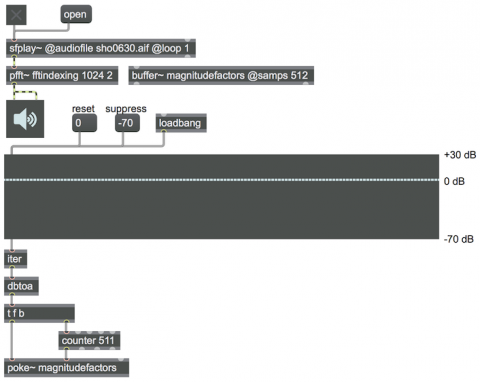
In this example, the fftindexing subpatch that we’ve written for the pfft~ object multiplies the magnitude value of each frequency bin by the corresponding sample in a buffer~ named magnitudefactors. The index numbers of the right outlet of fftin~ acces the buffer~ via the index~ object, to read a value from the buffer that gets used as a multiplier for the magnitude value. So, in effect, the contents of the buffer~ magnitudefactors are like a graphic equalizer function, modifying the amplitude of each of the bins. The results are fed into a poltocar~ object, along with the unchanged phase values, to convert them back to real and imaginary values for the IFFT process of fftout~, and the result of that is sent out of pfft~ as a modified audio signal.

Back in the main patch, we’re using a multislider object with 512 sliders to set those values within the buffer~. The values in the multislider are in decibels (a better format for the user interface), which are then converted one-by-one to amplitude factors to be stored in the buffer~ by the poke~ object. Thus, that portion of the patch is the user interface of the graphic equalizer, which modifies the sound in the frequency domain within the pfft~.

You can play the suggested sound file (or any other sound file), then begin changing the sliders of the multislider to change the strength of the different frequencies of the sound. To hear the process better, you might try suppressing all the frequencies by setting them all to -70 dB, and then bring up the amplitude for a few individual bins. If the sound source is rich enough, you’ll hear a very narrowly multiple-bandpass-filtered version of the sound.