Comb filter

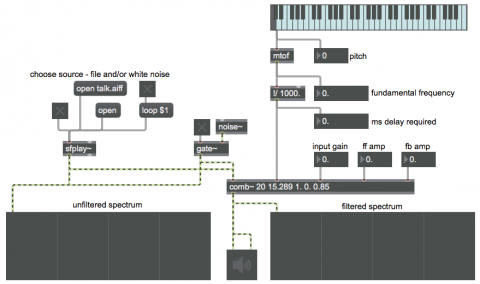
When a sound is mixed with a delayed version of itself, each sinusoidal component of the delayed sound has a unique phase offset compared to the original, so each frequency is accentuated or attenuated differently. For example, if a 1000 Hz sinusoid is delayed by 1/1000 of a second (1 millisecond), the original and the delayed version will still be perfectly in phase, so that frequency will be increased in amplitude when the two versions are added together. However, if a 500 Hz tone is delayed by the same amount of time (1/1000 of a second), the original and the delayed version will be precisely out of phase so that frequency will be canceled entirely when the two are added together.

In the first case the delay time is the inverse of the frequency (1/000 of a second is the inverse of 1000 Hz), so the delay time is the same as the period of one cycle of the wave, and thus the two waves are in phase. In the second case, the delay time is exactly one half of the period of the wave, so the two waves are exactly out of phase. This relationship between delay time and phase offset for a particular frequency (and all whole number multiples of that frequency) is the principle that forms the basis of a comb filter. The inverse of the delay time determines what frequency (and its harmonics) will be emphasized. When the output of the comb filter is fed back into its input, those frequencies are further reinforced, such that the spectrum has evenly spaced amplitude peaks that look like the teeth of a comb.

In this patch, we use the mtof object to convert a MIDI pitch number into its corresponding frequency, and then we take the inverse of that (divide it into the number of milliseconds in one second) to determine the number of milliseconds of delay for the second inlet of the comb~ filter object. The last argument (and last inlet) of the comb~ object determines how much of the output will be fed back into the filter, determining how much the resonant frequencies will get reinforced. Because the accentuated frequencies are all harmonics of that fundamental frequency, the filter imposes a sense of that fundamental pitch onto any input sound.