Basic linear mapping

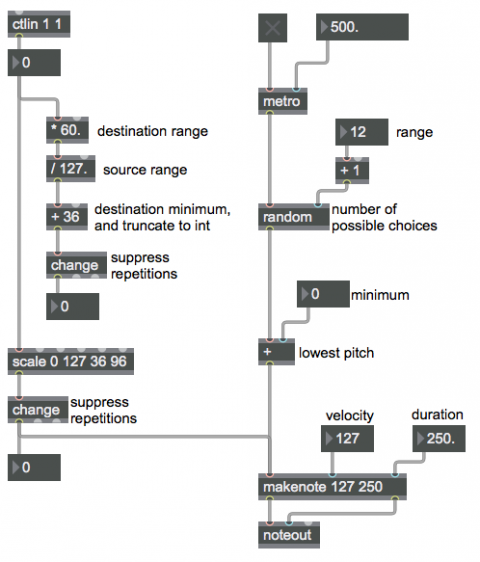
The most direct way to convert one range of numbers into a different range of numbers is a process called linear mapping. For each number in a source (input) range, find the corresponding number in a destination (output) range. The process is to multiply the input value by the size of the destination range (destination maximum minus destination minimum) divided by the source range (source maximum minus source minimum), then add the destination minimum to that. In short, the conversion operation involves scaling and offsetting: one multiplication and one addition.

The scale object does this for you. In this example we want to convert the incoming MIDI control data from the mod wheel of a synthesizer, ranging from 0 to 127, into a usable pitch range from 36 (cello low C) to 96 (flute high C). The patch demonstrates the use of the scale object, and also demonstrates that you can obtain the same result with basic arithmetic objects. Notice that, because there are no arguments with a decimal point in the scale object, the result is sent out as an integer. For a floating-point result, at least one argument of scale must be a float. The patch emulates that behavior by using an integer addition in the + object, which truncates any fractional portion of the number coming from the / object. Because the input range is greater than the output range, and we're dealing only with whole numbers, there will be some duplication of numbers in the output, so we filter out repetitions with the change object.

A similar process can be used to get any range of random numbers we want. First we establish a range of random numbers (for example, if we send 6 into the right inlet of the random object, the range of its output will be from 0 to 5), then we offset it by whatever value we want to be the minimum result.