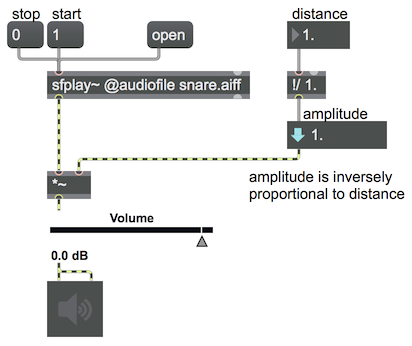
Amplitude is inversely proportional to distance
Our tympanic membrane (a.k.a. our eardrum) and a microphone are both devices that measure sound intensity. When a sound arrives at our eardrum or at the diaphragm of a microphone, either of which has a certain surface area, the power in that area (i.e. the intensity) is detected. However, the intensity of a sound, as measured by an eardrum or a microphone, will differ depending on the distance from the sound's source, because the sound is being emitted from the source in all directions. If you think of the sound energy as radiating outward from the source in a spherical pattern, and you bear in mind that the surface of a sphere is proportional to the square of its radius (the surface area of a sphere is equal to 4πr2), you can understand that the intensity of a sound as measured in a given surface area is inversely proportional to the square of the distance of the point of measurement from the sound source. This principle is known as the inverse square law: intensity is inversely proportional to the square of the distance from the source (I ∝ 1/d2).
Our subjective sense of a sound's "loudness" is not the same as its intensity, but is generally roughly proportional to it. But what does that mean in terms of the amplitude factor we'll use to alter a sound's intensity in digital audio? As defined in physics, the intensity of a wave is proportional to the square of its amplitude (A2 ∝ I). So that means that if we want to emulate the effect of a sound being twice as far away, (1/4 the intensity), we would need to multiply the amplitude by one-half. Indeed, based on what we know about the relationship between distance and intensity (the inverse square law, I ∝ 1/d2), we can see that the relationship between distance and amplitude is simply A ∝ 1/d; amplitude is inversely proportional to distance.
This patch shows how you can emulate a change of distance simply by changing its relative amplitude inversely. Of course, our sense of distance is also affected by reverberation and high-frequency rolloff, but this basic relationship between distance and ampitude is useful to know for sound spatialization.