
Figure 1. Classic hemiola, implying two tempi with a ratio of 3:2.
Department of Music, University of California, Irvine, USA
dobrian@uci.edu
http://music.arts.uci.edu/dobrian
Proceedings of Korean Electro-Acoustic Music Society's 2012 Annual Conference (KEAMSAC2012)
Seoul, Korea, 26-27 October 2012
Digital computers offer unprecedented flexibility and accuracy for the composition and performance of polytemporal music involving multiple time streams: polyrhythms, metric modulations, multiple tempi, and precisely calculated independent continuous tempo changes (accelerandi and decelerandi). This article addresses some important musical and technical issues encountered in music with multiple simultaneous tempi, including music with independently fluctuating tempi. The article includes a brief summary of some important precedents in pre-computerized music, a look at some implementations of polytemporality in computer music, and some suggested techniques for designing and manipulating multiple time streams in computer music composition.
October 27, 2012 is the centenary of the birth of American-Mexican composer Conlon Nancarrow. Nancarrow's body of compositions for player piano is the most concentrated exploration of polytemporal music -- music that proceeds with multiple independent beat rates. His painstaking work with mechanized pianos was an important precursor to computerized musical performance with Music N scores and MIDI sequences, and it demonstrated the conceptual and practical potential of polytemporal music. Computers now offer unprecedented flexibility and accuracy for the composition and performance of music involving adventurous exploration of multiple time streams--polyrhythms, metric modulations, multiple tempi, and precisely calculated independent continuous tempo changes (accelerandi and decelerandi)--yet the methodology of composing with these techniques has not been very extensively documented or theorized. In this article I summarize some obvious musical implications of polytemporality, and I will show some basic examples of its implementation in computer music.
Some Terminology
In this article I use the word time as a shorthand to refer to ways of measuring sequences of events. The most objective type of time measurement, the one most frequent in everyday discourse and scientific measurement, is the use of a regular, reliable and agreed-upon clock; I refer to this as clock time. Music is not commonly organized by direct reference to clock time, but instead uses a different type of time measurement known as musical time, which relies on an agreed-upon more-or-less constant unit of time known as a beat. The relationship of musical time to clock time is based on the rate of the beat--the number of beats that occur in a certain amount of clock time, commonly beats per minute (BPM)--known as the tempo. The onset time of each sonic event is the moment when it is perceived to begin, and its duration is how long it lasts; either may be measured in clock time and/or musical time. Any instant in time can be ascribed a unique numerical value in either clock time or musical time relative to an established 0 point; such a representation of a single moment is called a timepoint.
Some History
Perhaps the oldest and best-known compositional technique that evokes multiple time streams is the classic technique of hemiola, originally used to describe a situation in which three equally-spaced notes in one voice occur in the same time as two equally spaced events in another voice [Figure 1].

Figure 1. Classic hemiola, implying two tempi with a ratio of 3:2.
In actual usage the 3:2 ratio may be expressed not only by individual notes but by any grouping of notes that -- by its melodic contour or its harmonic implications -- can be considered to express a unified event with a duration 3/2 or 2/3 as long as another event [Figure 2].

Figure 2. Melody vs. harmonic rhythm establishes a ratio of 3:2.
Although originally applied only to this simplest of prime ratios, the term came to be used more generally to refer to any musical situation that suggests two different metric interpretations [Figure 3].

Figure 3. Pitch contour vs. dynamic accent implies a ratio of 3:4. .
Ratios with larger numbers, especially when occurring within a single measure or a single beat are more commonly referred to as cross-rhythms or polyrhythms [Figure 4].

Figure 4. Polyrhythms 5:4, 3:4, and 5:8.
Nancarrow employed hemiola extensively in his 1940 instrumental Trio for clarinet, bassoon, and piano (Nancarrow, 1991), and combined hemiolas and polyrhythms in his 1945 String Quartet No. 1 (Nancarrow, 1986). He continued to use these techniques in his studies for player piano, predominantly focusing on prolation canons in which the voices proceed at entirely separate tempi.
The prolation canon, also known as mensuration canon, in which a melody is performed in imitation but with augmented or diminished rhythmic values, dates back at least to Johannes Ockeghem's Missa prolationum in the Renaissance (Plamenac, 1966). As a compositional technique, prolation canon is related to hemiola, because the stretched or compressed versions of the melody imply different meters and/or rates of performance.
Nancarrow frequently composed mensuration canons in which the rates of the different voices are in harmonic ratios. Some of his studies for player piano exhibit relatively simple ratios such as 3:4 in Study No. 15, and 4:5 in Study No. 14. As his use of the technique grew more advanced and experimental, he employed higher ratios such as 14:15:16 in Study No. 24, 17:18:19:20 in Study No. 36, 21:24:25 in Study No. 31, and even 60:61 in Study No. 48. His most adventurous piano piece, Study No. 37 is a canon in twelve voices, each at a different tempo (Gann, 1995). In such a complex polyphonic work, the effect for the listener is no longer so much the perception of polyrhythm as of the gestural or textural effect produced by the relationships of simultaneous slightly different tempi.
Iannis Xenakis (1955) observed the potential for textural perception of polyrhythms in dense polyphony, and he employed simple polyrhythms of 3:4:5 in his 1956 composition Pithoprakta (Xenakis, 1967) to obfuscate the listener's sense of a beat. Because the numbers 3, 4, and 5 share no prime factors, the simultaneity of triplet eighth notes, sixteenth notes, and quintuplet sixteenth notes yields 11 unique attack points within each beat. By writing syncopated rhythms with those beat divisions in dense polyphony, he achieved clouds of notes that are so complicated they seem beatless. He thus used polyrhythms not so much to create a sense of polytemporality, but rather in an attempt to obscure traditional beat-based musical time.
Truly polytemporal instrumental music in which the players must maintain separate tempi with rigorous precision in order to arrive in synchrony at specific moments is difficult to perform because humans have an imperfect sense of musical time. When players are working together in a common musical time stream, they maintain synchrony by constantly and flexibly adjusting their tempo as needed to maintain a group consensus. However, if individuals or subgroups of an ensemble are called upon to maintain a separate and perfectly exact tempo while others do likewise in a different time stream, it can be difficult to adjust to small fluctuations in other time streams. One solution is for the musicians to listen to pre-recorded click tracks to ensure accuracy within each time stream, or to have multiple conductors charged with coordinating the different tempi. A notable example of this approach of using multiple leaders is Karlheinz Stockhausen's 1957 composition Gruppen (Stockhausen, 1963) for three orchestras and three conductors.
Terry Riley's 1964 composition In C (Riley, 1989) for any number of players (he suggests about 35) establishes an unflinchingly regular base tempo with constant repeated eighth notes in the highest register. Against that constant rhythm, other instrumentalists repeat musical cells of different lengths, almost all of which are some whole number multiple of the eighth note duration. Each player's musical time is synchronized to the same "master clock" of the repeated eighth notes, but s/he is at liberty to repeat each cell any number of times. The result is a music that is very clear in its global tempo, yet consists of a constantly changing, massively polyphonic conglomeration of hemiolae. With a single page of notation and this simple use of indeterminacy--allowing each player the liberty to choose the number of repetitions for each cell--the composer allows for an infinite number of possible realizations, each of which is nevertheless still identifiable as the same composition.
Steve Reich, in his 1960s tape compositions It's Gonna Rain and Come Out, took musical advantage of the effect of two nearly-identical-length cycles gradually going increasingly out of synchronization. Initially the cycles (tape loops) are in seemingly perfect unison, but one of two cycles is in fact ever-so-slightly longer than the other, such that the temporal relationship between the two unison sounds gradually shifts. The effect is at first one of comb filtering, as the component frequencies of the sounds themselves constructively and destructively interfere based on the time of the delay. As the delay between the two sounds increases, the effect becomes a timbral blurring, then a short but discrete "slapback" echo, and eventually a new composite rhythm.
In the case of these two pieces, the compositional technique was derived from Reich's experimentation with tape recorders, and was the result of the practical impossibility of perfectly synchronizing tape loops on two different players. Gradually increasing asynchrony, as found in these compositions, can be caused by a slight discrepancy in the length of the loops, or by a discrepancy in the speed of playback. In either case, the two sounds have a slightly different periodicity of repetition. A discrepancy in playback speed has the side effect of creating a discrepancy in tuning as well as in periodicity. Careful analysis of Come Out (Reich, 1987) indicates that the loops were playing at very slightly different speeds. It is quite easy to play the same sound at two subtly different rates in a program such as Max [Figure 7].
These experiences led Reich to compose similar gradual tempo shifts into some of his instrumental compositions--notably Piano Phase (1967) and Drumming (1971) from the time period immediately following those tape works. The compositions require the performers to, in a sense, emulate the behavior of the two tape recorders playing at slightly different tempi; one performer speeds up imperceptibly until s/he is exactly one rhythmic unit (e.g., one sixteenth note) ahead of the other performer.
Huijae Chung, in his composition titled Multi Tempi 21, employed temporal canon at the unison with tempo ratio close to 1 in a highly polyphonic texture. The music consists of an ascending eight-note piano melody repeated over and over, played at 21 slightly different tempi evenly spaced between 120 BPM and 110 BPM. All tempi thus reside within a 1.091:1 ratio. The recording was made with digitally sampled individual piano notes triggered by MIDI; the MIDI data was played at a different tempo for each of twenty-one different channels of a multi-track audio recording, thus triggering the exact same sounds at different rates without causing any mistuning of the sounds themselves.
Because of the number of voices and the range of different tempi, timbral blurring begins with the very first note, discrete echoes can be discerned within seconds, and clear polytemporality and resulting composite rhythms are heard soon thereafter. Due to the large number of voices in very high rational tempo relationships such as 240:239, 239:238, etc., the music passes through a wide variety of constantly changing textures and rhythms, and the music never truly repeats within the seven and a half minutes that Chung lets the process run its course. There is an initial divergence point at the beginning, but no true convergence point of the different cycles. There are, however, frequently moments in the composition when enough voices briefly achieve near-synchrony to give the impression of concerted behavior.
The Whitney Music Box web application (Bumgardner, 2006) demonstrates repeated tones played (and visually displayed) at 48--or in some instances as many as 120--separate harmonically-related tempi. The program was inspired by the ideas presented by John Whitney (1980) relating musical and visual harmonicity. As one might expect with so many voices, the resulting sounds are often textural as much as they are explicitly rhythmic, but because of the strictly harmonic relationships between tempi there are frequent convergence points of varying degrees of unanimity, providing for sonic variety and long-term rhythmic formal structure.
In practice, the time streams in polytemporal music are often not purely independent, because the different tempi are chosen in such a way as to relate to some slower global tempo at a larger structural level, or to create specific convergences between disparate time streams. In the music of Nancarrow, the musical tempi are almost always chosen in specific harmonic ratios, even if those combinations may be extremely complex or may consist of ratio relationships that are very obscure. Even his Study No. 21--known as "Canon X" because one of its two voices is constantly accelerating while the other is constantly decelerating, and the pitch range of one voice descends while the other ascends--is carefully designed so that the voices have a known point of convergence in the middle and the two melodies occupy the desired amount of time for the particular musical form. It is relatively rare--at least in the examples reviewed here--that the tempi in a piece of music are purely independent with no shared reference.
One might argue that simultaneous independent time streams are not inherently musically interesting if they are totally unrelated (Nemire, 2012). The simple fact that two things coexist simultaneously and appear to be oblivious of each other can be expressive in its own right; truly free counterpoint might serve as an expression of liberty and independence, for example. And such complete independence can lead to interesting coincidental simultaneities and juxtapositions. But polytemporal music with no discernible points of convergence or divergence does not necessarily require any particular composition or control. The point of using a computer to realize polytemporal music is to leverage the computer's powers of calculation and its precision of performance. The computer can potentially aid the composer in realizing polytemporal music with specific tempo relationships and/or specific desired points of convergence.
Commercial software
Despite the applicability of computers for exploring and realizing polytemporal music, very few commercial computer music applications provide for the specification of time in multiple, different, simultaneous time streams. This is understandable, since the vast majority of all music takes place in--and is largely conceived as--a single time stream. Because of the scant user demand for polytemporal control, it is presumably not commercially viable for music software companies to devote valuable programmer time to implementing multiple time streams, in the form of multiple transport mechanisms, as a function of a common music application such as a DAW (e.g., Pro Tools). One can, of course, perform digital audio processing operations in nonreal time such as audio rate change, time compressions or expansion, trimming, and looping, and these operations have been made ever easier in many audio and music programs. In that sort of nonrealtime processing, the computer is helping with sound modifying operations but is not particularly helping with the calculations necessary to implement those operations in a composition.
Within the paradigm of a single master transport controlling the passage of time, the Live application by Ableton performs high-quality time compression/expansion in real time to adjust the duration of live recorded or prerecorded sounds to a certain number of measures in a given tempo. Those time-adjusted sounds can then be exported to new audio files for use in polytemporal composition. Live also provides the capability to play simultaneous loops of different lengths, thus achieving hemiola-like effects with audio loops.
By and large, though, exploration of polytemporality remains predominantly the province of computer music programming environments such as Csound, Max, Pd, and SuperCollider. Even these specialized and relatively esoteric programming environments are, quite understandably, mostly modeled on a single unifying sense of time related to, or based directly on, clock time.
Recent development, spearheaded by David Zicarelli, in the Max programming environment (Puckette, 1990), facilitates polytemporal music. I will briefly present the conceptualization of multiple time streams that underlies the implementation of tempo-relative musical timing in Max, and I will provide specific examples in Max showing simple applications of compositional techniques for hemiola, polyrhythms, polytemporality, and the use of transfer functions for predictable timepoint warping in multiple time streams.
Simple implementations in Max
Hemiola with audio loops. The ability to build constantly changing textures with loops of different lengths exists in many commercial programs. In Max one can write a program that permits the construction and modification of such textures on the fly. For example, one can play multiple simultaneous instances of the same sound, yet loop a different duration segment of that sound in each voice of a polyphonic texture. Segmenting a few seconds of sound, which may well contain its own internal rhythms, into segments with durations in a ratio 13:14:15:16 is a simple way to make an evolving rhythmic texture out of a single sound [Figure 5].
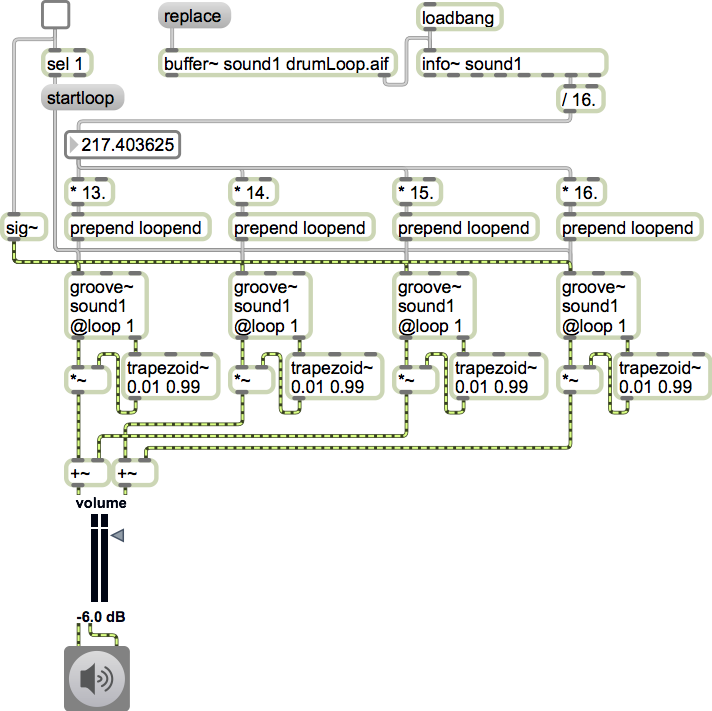
Figure 5. Four loops with lengths in the ratios 13:14:15:16.
Flexible, related tempi. The capability to to implement polytemporality has in fact always existed in Max. The canonical timing object metro runs with as much clock time precision as is available in the operating system, so with multiple metros one can trigger events at any combination of rates, and polyrhythms can be enacted with some simple arithmetic calculations. The tempo object makes those tasks even simpler by allowing the quarter note tempo to be specified in BPM and by allowing the whole note to be divided by any ratio of whole numbers up to 96.
Using multiple independent transport objects to control sets of timing objects, one can run entire timed processes at independent rates. The transports can progress completely independently or they can be controlled by a common global tempo. For example, with three differently named transport objects, one can easily play the same composition at three different tempi, readily producing a tempo canon. If the three transports are running at related tempi, a common global source can modify all three tempi at the same time, again using simple arithmetic to determine the correct tempo for each one [Figure 6).
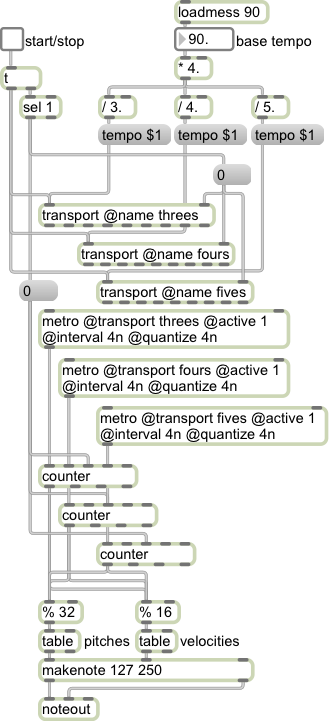
Figure 6. Tempo canon with the ratio 3:4:5.
Rate change in audio playback. In the spirit of Reich's Come Out, one can achieve interesting sonic effects such as phasing and chorusing by playing the same sound at two or more subtly different rates. The slight mistuning caused by the rate changes, combined with the slight delay that results, causes interference between the two sounds, resulting in filtering and blurring effects as well as slapback echos as the sounds go further out of synchonization. This is a computerized example of temporal canon at the unison, using a ratio of two tempi--two audio playback rates--that is extremely close to 1 [Figure 7].
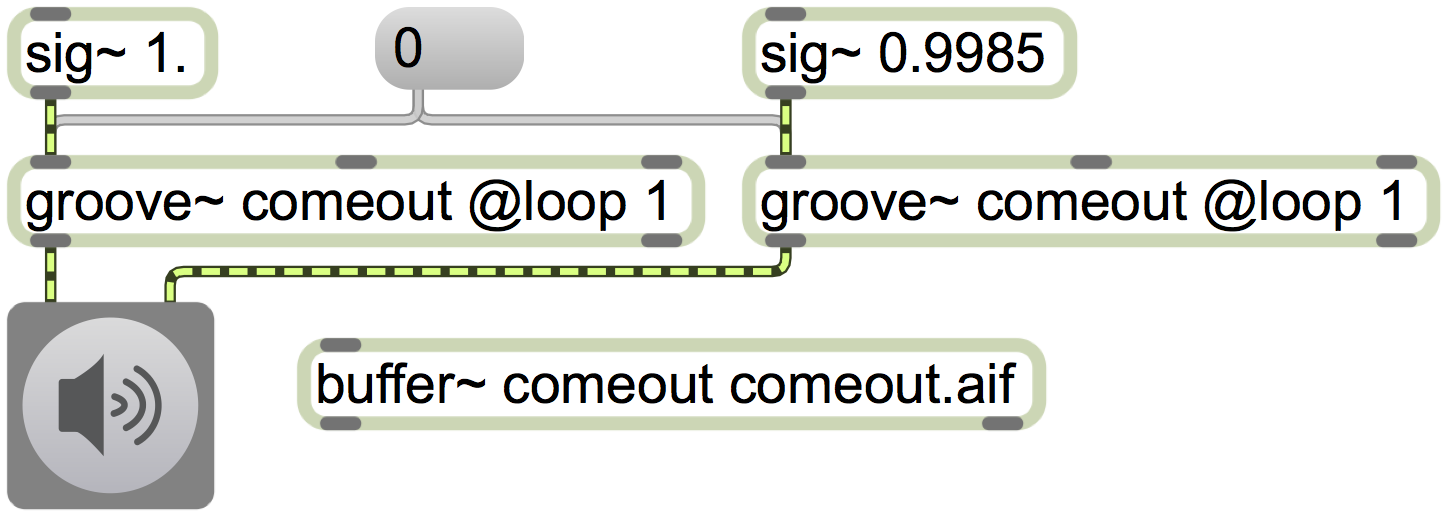
Figure 7. A sound looped in two channels with a 0.15% rate discrepancy.
Continuously variable tempo relationships
One asset of the computer is its ability to calculate and enact discrete tempo changes instantaneously and precisely. Getting the computer to play with tempo rubato (flexible tempo), or to follow a desired curvature of acceleration or deceleration, is a bit more complicated but still feasible.
The Csound computer music programming language (Vercoe, 2008) provides a straightforward relationship between objective clock time and the musical time described in its score files. Starting times and durations of events are specified in musical time units that are inherently undefined but that are related to clock time by a tempo (rate in units per minute) and are often referred to as "beats", just as in common practice Western music notation. Musical timings may be expressed using decimals with a fractional part (e.g., 1.875 units) to specify time with an arbitrary degree of precision. The musical time unit is converted to clock time with the simple formula 60./M, where M is the tempo specified in units per minute. By default the tempo is 60 BPM, causing the units to correspond exactly with seconds in clock time. If the tempo is explicitly specified other than 60, musical time can proceed independently of clock time, with units being converted to their corresponding clock time value.
It's significant that in Csound the tempo markings of a section of music are all provided in a single statement that is pre-processed before the sound itself is computed. The statement can specify as many tempo changes as desired, each of which is tagged with its own start time. These start times must be presented in non-decreasing order. The start time of each tempo indication is specified in musical time units, the actual clock time of which is dependent on whatever tempo indications occurred earlier. Tempo can be changed discretely (i.e., instantaneously), or gradually by linear interpolation between two tempo specifications. If a tempo indication is the last one of a given section, or if it is followed by subsequent indication of the same tempo, the musical tempo will remain constant. If a tempo M1 is followed by a different tempo M2, the tempo changes linearly, beat-by-beat, from M1 to M2. (Verco, 1992) Because the start time of each tempo change is specified in musical time rather than clock time, each tempo indicator can be thought of as a point in a tempo graph, a graph which is itself nonlinear (with respect to clock time) on its time axis due to the duration-changing effect of each tempo. The nonlinear x axis of such a graph makes it fairly difficult for a human composer to predict the precise clock time duration of a complete passage that contains many tempo changes, accelerandi, etc., but the computer calculates it with ease. The composer learns the clock time result retrospectively by consulting the duration of the computed sound file.
Tempo-relative timing. In realtime programming environment such as Max, the problem of accurately realizing constantly changing tempi, and of predicting convergences of multiple flexible time streams is all the more challenging. Events in Max are governed by an always-active scheduler based on an inflexible objective clock. Immediate or future events may be scheduled--either explicitly by the user or automatically by a timing object such as metro--at any time. The events are usually produced in real time or scheduled on the fly, not foreseen as they would be in a pre-composed score. Thus, the implementation of tempo-relative musical timing into the existing Max timing objects, based on the transport and its related objects, presented some special challenges to the programmers of Max itself.
The underlying Max scheduler must remain inflexible and reliable because its solidity is the foundation upon which all timing in Max is based. The Max scheduler is a time-sorted list of all the things Max has to do. The head of the list--i.e., the event scheduled for the most proximate future moment--is dealt with next. In addition to the main scheduler, there can be tempo-relative timed events managed by the transport system. In Max there is one global transport for managing tempo-relative timing, but one can also program any number of additional independent transports, each identified by name, allowing for a potential multitude of independent time streams.
Tempo-relative timepoint events are stored in a separate time-sorted list managed by the relevant transport. If the tempo of that transport changes, Max must change the timing of the events in that list, taking into account the time that has elapsed since the events were first posted to the list. These transport-related lists of events are all separate from the main Max scheduler. The main Max scheduler therefore needs only one scheduled event for each transport, namely a time tag telling it when it next needs to consult the transport's list (Zicarelli, 2012).
Timepoint stretching. The principle that underlies tempo rubato is that the tempo of the different voices of a composition might flex subtly, with the performer(s) nevertheless remaining aware of the other voices so that an important global tempo is maintained. If one voice "steals time" by speeding up or slowing down relative to another voice, either the other voices must do likewise to stay synchronized, or that stolen time must be "given back" by flexing the tempo commensurately in the opposite direction. The assumption of synchrony is that all tempi are constantly in a 1:1 relationship, but if that ratio changes slightly for a time, it must be changed in an opposite manner for a comparable amount of clock time in order for the two tempi to resynchronize.
From this standpoint, we can compare all timepoints in two different time streams using a transfer function, also referred to as a lookup table. That is, for each event that occurs in one time stream (an incoming x value), we can use a transfer function to look up the corresponding timepoint (y value) in another time stream. This lookup table for timepoints has also been called a time map (Jaffe, 1985).
A comparison of all timepoints in two perfectly synchronized time streams is a linear (unity) transfer function (Figure 8]. With a linear transfer function all the musical time points have the same clock time.
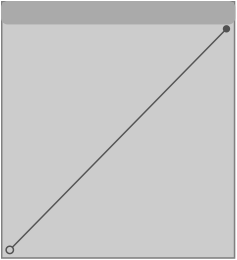
Figure 8. A linear function with a slope of 1:1 causes no distortion.
As long as the transfer function begins at point 0, 0 and ends at point 1, 1, the two time streams will be synchronized at those points. Additional convergence points will occur whenever the transfer function crosses this unity line.
In a realtime situation the slope of the transfer function must always be between 0 and 1; the x and y values both must always be increasing, meaning that time is progressing in both time streams. In a nonrealtime evaluation, such as evaluating a precomposed score before attempting to perform it, one could employ a model in which musical time (score time) could actually move backward, such that events that occur later sequentially in one time stream occur in reverse order in the other time stream; however, in a realtime situation where we are determining all time points sequentially, this is not practical. Therefore, when implementing this idea in Max, we will confine ourselves to transfer functions that are always increasing on both axes.
To understand how this timepoint lookup method will work with a nonlinear transfer function, let's consider a lookup table in which the function is made up of straight line segments [Figure 9].
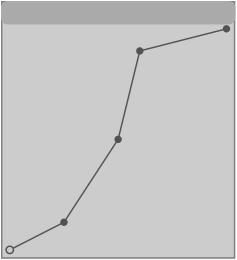
Figure 9. Breakpoint line segments for a timepoint transfer function.
In this example, the function begins at point 0,0, proceeds linearly to 0.25, 0.125, converges with unity at point 0.5, 0.5, goes to point 0.6, 0.9, and resolves at point 1,1. As time stream x proceeds from time 0 to time 0.25, time stream y proceeds from 0 to 0.125. The slope of this line segment is 1:2 so all timepoints in stream y up to that point will have 1/2 the value of the corresponding timepoints in stream x. One could also think of this as meaning that the musical tempo of stream y is 2 times that of stream x, but for this discussion we will be focusing on the timepoints rather than the tempo, since that is what is depicted by the function. As time stream x progresses from 0.25 to 0.5 (a difference of 0.25), time stream y progresses from 0.125 to 0.5 (a difference of 0.375). Between those two points, the slope is 3:2, so during that span of musical time the timepoints in stream y are spaced with 1.5 times the distance as those of stream x (i.e., musical time elapses 2/3 as fast in stream y as it does in stream x). Between times 0.5 and 0.6 in stream x, time progresses from 0.5 to 0.9 in stream y (yielding a slope of 4:1), and in the remaining time from 0.6 to 1 in stream x, stream y progresses from 0.9 to 1 (a slope of 1:4). This means that if the musical time of stream x were, for example, constantly 60 BPM over a time span of 60 seconds, stream y would at first have a tempo of 120 BPM for 7.5 seconds, then 40 BPM for 22.5 seconds, then 15 BPM for 24 seconds, then 240 BPM for 6 seconds.
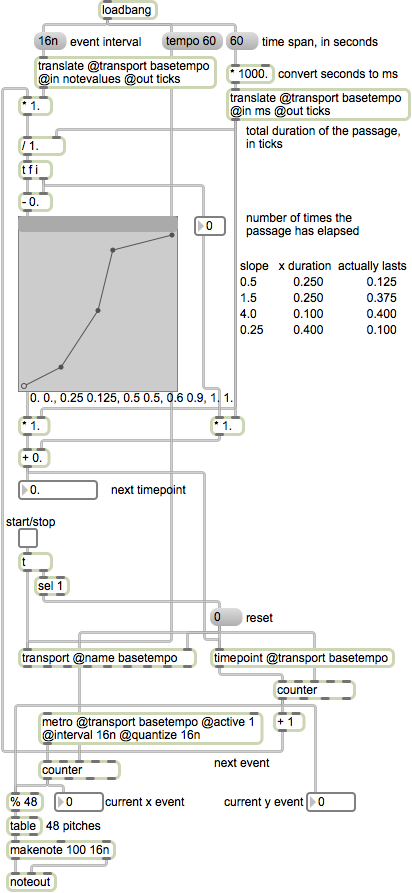
Figure 10. An implementation of a timepoint transfer function in Max.
How can one implement this in Max using tempo-relative timing without manually doing all the foregoing calculations? At each event that occurs in stream x, we can use its timepoint to look up the corresponding y value for the next scheduled timepoint to determine when that timepoint should occur in stream y. For example, if stream x is scheduling events every sixteenth note in its own musical time with a metro, it can look up the time of the next scheduled event in the transfer function to set the timepoint for that event to occur in stream y [Figure 10]. In this example, a metro designating those events in stream x steps through a table of pitches at a constant rate in its own musical time, which happens to be a constant rate in clock time as well because the tempo of stream x is constant, 60 BPM. The timepoint object is used to trigger each note in stream y, and is also used to look up the correct timepoint for the subsequent y event.
The time points in stream y initially have 1/2 the clock time value of those in stream x because the slope of the transfer function line segment is 1:2. Each time the slope of the line segment changes, the interval of the time points in stream y--all of which are equally spaced sixteenth notes in stream x--will change accordingly. By the time the designated time span of the function has elapsed--in this example, 60 seconds--the two time streams will reconverge, landing in perfect synchrony, in this case after 240 sixteenth notes have elapsed.
This technique for warping timepoints becomes more interesting when the lookup function contains exponential and logarithmic curves, which result in more gradual ritardandi and accelerandi [Figure 11]. A straight line segment produces a constant tempo; the exact warping effect of exponential and logarithmic curves depends on the slope of the curve at any given point, and where it is in relation to the central unity line. Again, as long as the beginning point and the ending point are on the unity line, e.g., 0, 0 and 1, 1, the two time streams will be synchronized at those points.
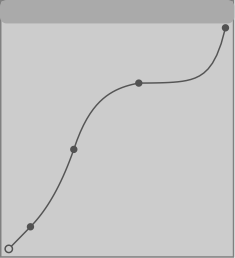
Figure 11. Logarithmic and exponential curves in the transfer function result in gradual accelerations and decelerations.
In this example, the time streams start in synchrony; the first segment of the function is a straight line with a slope of 1:1. The second segment is an exponential ritard (lengthening of the timepoints), the third segment is an acceleration (shortening of the timepoints) but still does not achieve the original tempo, and the final segment crosses the unity line at a high rate of speed before a final ritard to resynchronize with the x value. This type of gradual timepoint warping is arguably more expressive than the discrete shifts and constant tempi caused by straight line segments, and the accelerations and decelerations permit us to perceive the sort of phasing effect--the constantly changing relationship between the two or more time streams--that is reminiscent of the acceleration studies of Nancarrow and the early phasing works by Reich.
Time is our way of measuring sequences of events, and sound is music's way of articulating time. Every bit as much as sound, time is the material from which music is made. Musicians have been equally fascinated by both sound and time. Because composers make music in nonreal time--out of time, as it were--they have always had a particular interest in the intricate manipulation of time.
Conlon Nancarrow was an innovator in the composition of time, and a pioneer in the use of machinery to support his musical innovation. There is still much interesting work to be accomplished in the theory, taxonomy, and experimentation of time manipulation as a compositional technique.
Computers provide us with unprecedented resources for experimentation with musical time, not just for increased precision--although they certainly do facilitate that--but also for experimenting with the very plasticity of time and the role of polytemporality in music.
It is my hope that this essay on polytemporality, presented in the context of a computer music conference on the centenary of Nancarrow's birth, might point to the relevance of his ideas in the field of computer music, and might inspire practitioners of computer music to explore challenging new temporal aspects of music.
Bumgardner, Jim (2006). Whitney Music Box (web application). http://whitneymusicbox.org/
Chung, Huijae (2007). Multi Tempi 21. Premiered at Nong Project 2007, Seoul, Korea. http://huijaemusic.com/
Gann, Kyle (1995). The Music of Conlon Nancarrow. Cambridge, UK: Cambridge University Press.
Jaffe, David (1985). "Ensemble Timing in Computer Music". Computer Music Journal, 9:4, 38-48.
Nancarrow, Conlon (1986). String Quartet (1945). Baltimore: Sonic Arts Editions, Smith Publications.
Nancarrow, Conlon (1991). Trio (1940). Baltimore: Sonic Arts Editions, Smith Publications.
Nemire, Julie A (2012). "Convergence Points in Nancarrow's Tempo Canons". Online Symposium: Conlon Nancarrow, Life and Music. http://conlonnancarrow.org/symposium/
Plamenac, Dragan, ed. (1966). Johannes Ockeghem: Complete Works, vol. 2. New York: American Musicological Society.
Puckette, Miller, et al (1990-2011). Max (computer music programming environment). San Francisco: Cycling '74 (originally published by Paris: IRCAM).
Reich, Steve (1967). Piano Phase. London: Universal Editions.
Reich, Steve (1971). Drumming. New York: Boosey & Hawkes.
Reich, Steve (1987). "Come Out" (1966). Early Works. New York: Elektra/Nonesuch.
Riley, Terry (1989). In C (1964). New York: Associated Music Publishers, Inc. (originally published by Celestial Harmonies).
Stockhausen, Karlheinz (1963). Gruppen. London: Universal Editions.
Vercoe, Barry, et al (1991-2008). Csound (music programming language). http://sourceforge.net/projects/csound/
Vercoe, Barry, et al (1992). Csound Manual. Cambridge, MA: Massachusetts Institute of Technology.
Whitney, John (1980). Digital Harmony: On the Complementarity of Music and Visual Art. New York: McGraw-Hill Inc.
Xenakis, Iannis (1955). "La crise de la musique sérielle". Gravesaner Blätter, 1, 2-4.
Xenakis, Iannis (1967). Pithoprakta (1955-56). London: Boosey & Hawkes.
Zicarelli, David (2012). Personal correspondence with the author, September 5, 2012. Unpublished.